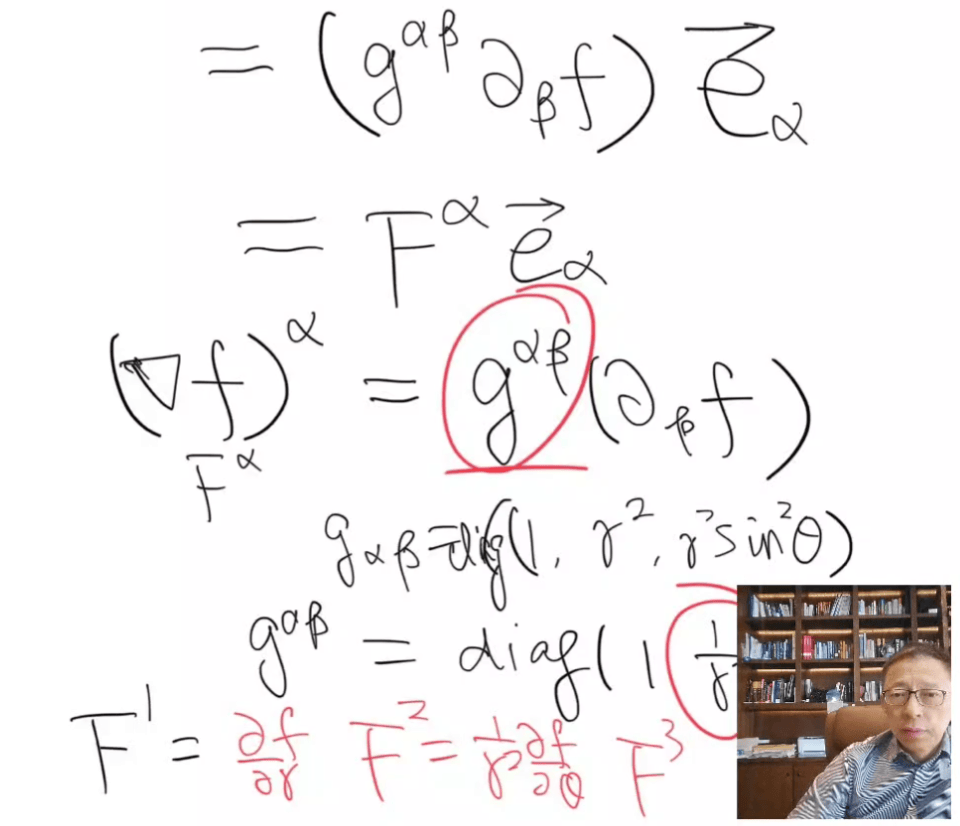如何使用协方差衍生物来描述梯度操作员和拉普拉斯操作员作用的标量字段的结果？在4月6日的12:00时，启动了“张乔阳的物理课”的243阶段。 Sohu的创始人，董事长兼首席执行官Zhang Chaoyang和博士学位都在Sohu Video Live广播室中。他从多元函数演算的角度介绍了梯度运算符的含义，然后从时态分析的角度解释了编写梯度运算符作为相反组件的需要。坐标的推导是通过协变量物质获得的，因此指标需要转换。最后，转换后的梯度运算符的相对部分是保留的，协变量衍生物运算符以获取拉普拉斯操作员。 。对于标量场F（x，y，z），如果磁点的点是由微小向量移动的，则在泰勒的多变量函数的帮助下，差异的变化-DifferenceF与坐标DR移动的F的书记可以写成扩展全文
它可以被视为两个向量的内部产品
在将梯度运算符应用于F之后，确定第一个支架中的方程式，并获得
同样，在球形坐标系中，可以通过球形坐标单元碱基向量扩展场字段的矢量数量。
那么f（r，θ，φ）的差异-bi变量可以写为
括号中的方程是由作用于f的球形坐标下的梯度操作员的结果。
该结果是在球形坐标系统下的载体计算中梯度运算符的表达。这是根据单位基础向量扩展梯度向量的表达。在张量综述中，对扩展坐标基矢量的向量表达的表达更多。在以前的课程中，球形库尔的单位基础矢量之间的关系引入了Dinates和坐标的基础向量。
用梯度操作员的表达替换
在最后一步，梯度向量再次标记为f。从上面的公式，我们可以看到球形坐标中梯度向量场的三个反向组件是
以上是从矢量计算的角度获得的梯度运算符的相对部分。接下来，我们将从男高音审查的角度回顾整个计算过程。首先，通过取协变量物质获得坐标中标量的部分导数，这是由坐标中的矢量基础扩展的系数。
位置向量元素中的NIT支持者，并可能捕获差异的变化量
最后一步使用上下底座向量的双重性。
要稍后找到梯度矢量场的协方差差异，需要将其转换为一条线相反物质和坐标下基载体的AR组合，以将其减少到协方差衍生物操作员并找到协方差差异。相反的成分是根据坐标扩展的系数。使用量表向量的二元基础的转换，上层矢量被相对尺度和下基矢量的缩合代替，以获得
仅将对角线元素用于逆变器仪表
那我知道了
球形坐标下的拉普拉斯操作员
标量的梯度是向量场。在发现差异之后，协方差变化了，它得到了标量磁场的结果，可以由拉普拉斯操作员起作用。
在三维直线空间中，球形坐标系的K-SHI符号为
第二个相等的签名利用了索引α和δ的对称性，这里的α和δ都是虚拟指标，因此您可以在f中替换第三项的α和δ第一行，然后使用比例尺的两个张量指标的对称性，您可以看到它是从第一项出现的。最后一个平等签名使用仅是对角线元件的球形坐标量规的性质，即
这样，每个项目都有四个α指标，这可能会在爱因斯坦总和协议下引起混淆，因此我投降了Eins Dementtetein和清楚地写出。
请注意，仪表只有对角线元素，意味着逆变器计等于协方差计的奖励
所以
更换标准后，您可以得到
由此，可以直接计算Kerry Talisman的三个部分
（Zhang Chaoyang计算差异 - 矢量场协方差）
用拉普拉斯操作员的表达式替换克里斯塔的符号以获得
这与矢量计算中获得的结果一致。
据了解，周日中午12点在SOHU视频中现场直播“张乔阳班”。网民可以Earch for“ Zhang Chaoyang”要“遵循Sohu Video应用程序的流”，以观看现场广播和过去时代的完整视频重播；请按照“张Chaoyang”物理课程帐户来查看课程中的简短视频；此外，您还可以在SOHU新闻应用程序的“ SOHU技术”帐户中阅读每个物理课程的详细文章。回到Sohu看看更多