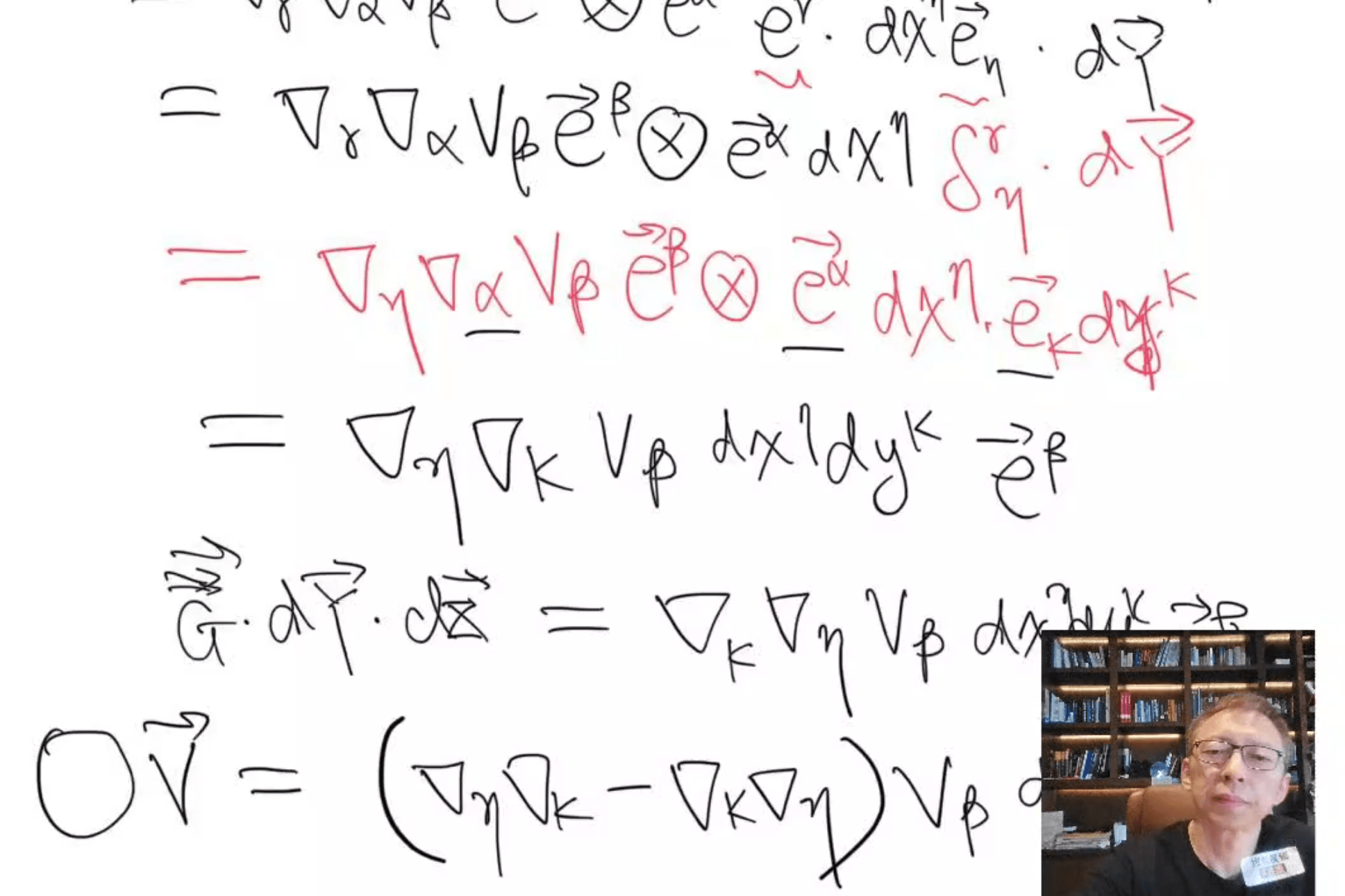如何理解空间和时间的曲率？如何描述张量中的路缘？在6月1日的12:00，“张乔阳的物理课程”是“ 248期”。最终，对于以下的微元素，Zhang Chaoyang介绍了以下衍生物的协变量。向量和扩展Of系数称为相反物质；或者它们可以通过上层载体扩展，并且系数的膨胀称为协变量。每个张量索引都可以选择两种类型的扩展方法之一，因此对于第二项以上的张量 - 符合键的张量，有不同的方法可以扩展。例如，二阶男高音的第二公式称为（2,0），也称为（2,0），第三个公式称为（0.2），第四和第四公式的指标全部向上和向上，共同称为（1,1）。至于三阶张量，有8种类型的扩展技术，该技术由相反的组件完全扩展，并由MGA协变量成分完全扩展。
张量的梯度
除张量本身外，人们还关心空间时间内的张量分布属性，或者在空间位置上更改男高音字段的速度。换句话说，多少当磁场的检测点移动向量元件的一小部分时，发生变化。这个小相位矢量微元素可以通过上下坐标和下坐标基矢量扩展为
对于标量场ϕ（x），它在此微小矢量中的变化量可以通过以梯度向量点的小矢量为小的矢量来表示。
其中，梯度向量扩展的基本形式是
对于字段向量v（x），更改位向量元素的值为
其中THED代表协方差习惯，该习俗与D在标量领域所代表的普通差异不同。向量的梯度是二阶张量，定义为
然后，它被位向量微元素撤回，并返回到一阶张量。您还可以清楚地替换基本矢量，以加深对“梯度和位矢量微元素收缩和更改张量的微元素”的理解”应该注意的是，这里的梯度张量有两个基本的向量。当执行梯度张量和位向量数字之间的点比例时，梯度张量中主要点再现的基础向量是与差异相关的E^γ，这并不混淆。从编写公式的角度来看，将小矢量元素放在梯度男高音的左侧可以自然地使其陷入小矢量的小元素上，因此在计算过程中，可以使这种写作感觉更有可能犯错。
由于向量的变化不仅应视为物质的变化，而且应视为基本向量的变化，因此矢量的梯度必须由协方差衍生物表示。
其中，克里由双基矢量表达。
首先将基本矢量推导的部分操作嵌入高维直线空间中，然后预计将返回到低维空间。此计算来自以前的类。有兴趣的网民可以回顾以前的文章。
现在已经知道，向量的梯度是二阶男高音。如果您想研究此二阶张量的该领域的分布，则需要计算二阶男高音的梯度。在本课程中，张·乔阳（Zhang Chaoyang）使用二阶张量的上矢量扩展公式来计算二阶男高音的协变量的习惯。
第三个方程式取代了愚蠢的指示器。从计算结果来看，二阶张量的协变量等于第三阶男高音和某种矢量微武器的凝结。上述公式中的冷凝指数为γ。该三阶张量称为二阶张量梯度。本文使用G进行标记。其向量的上部扩展公式是
首先知道Riemann曲率的张量
掌握梯度计算后tOOL，您可以朝Riemann曲率张量移动。 Assume that there is a field vector V (x) in space, thatExamines vector V (P) in the field of field P. First walk the observation point along with X direction for a short path ① to point S, then walk a short path ② to point Q in the direction of Y, and first walk a short path ③ to point T in the direction of Y, and then walk a short path ④ to point the Q in X direction. Vector V的协方差分化通过两种方式计算得不均匀。本节试图减少差异的表达 - 从向量的扩展公式的角度来看，差异是不同的，并且在下一课中要解释特定的计算。
（自定义的两个计算路径）
沿路径①行走DX（P）后，向量V差为
然后遵循路径②，差异的变化 - 我不同的原因是
这里的位矢量元件dy是通过沿点P的dy（p）沿使用DX，它本身在翻译过程中不会改变。但是，值得补充的是，鉴于弯曲的时空，翻译产生的向量与向量相等的组件不直接匹配，因为不同位置的基本向量不一定相等。要了解翻译向量的组件是如何连接的，我们必须从协变量将其与翻译路径一起区分的条件开始。为了使写作方便而清晰，矢量微元素的位置临时用字母y标记，从而满足y的另一侧
这意味着
将dy更改为y（s）-y（p），然后更改为dy以获取
通过这种方式，点P点的向量部分可能会表达位置向量转换为S。可以添加或减去，可以考虑 - 智慧
作为初始推导，可以写入路径②形成的向量V的差。
另一方面，在遵循路径③dy（p）指出t之后，向量V的变化为
而差异的变化是由路径中的q点引起的，
从这里我们可以得到
平等签名的右侧是P点中指定的所有数量，因此您也可以在接下来放弃它。其中，第一个项目
第二项是
这样，您会知道会有差异 - 通过走①②路和走路，是扣押的kulan的差异。
这正是Riemann曲率张量的确定公义的起源
据了解，周日中午12点在SOHU视频中现场直播“张乔阳班”。网民可以搜索“ Zhang Chaoyang”来“遵循Sohu视频应用程序的流”来观看直播以及过去时间的完整视频重播；请按照“张Chaoyang”物理课程帐户查看“知识”点数简短的视频；此外，您还可以在SOHU新闻应用程序的“ SOHU技术”帐户中阅读每个物理课程的详细文章。回到Sohu看看更多